2.6 The Mole
The mole (n) is defined as the amount of a substance that contains as many elementary entities as there are atoms in exactly 12 g of carbon–12. This experimentally determined number is called Avogadro’s number (NA)
\[1~\mathrm{mole} = 6.022\times 10^{23}\] Molar mass is the mass (in g) in 1 mole of a compound or element given in units of g mol–1. One mole of some familiar substances:
- 4.0 g of He
- ~18.0 g of H2O
- ~26.98 g Al
- ~63.55 g Cu
- ~58.44 g salt (NaCl)
- ~180.16 g sugar (C6H12O6)

1 mole of marshmallows would be enough marshmallows to make a 19 km (12 mi) thick layer of marshmallows covering the entire face of the Earth. (Marshmallows would be in the clouds)
1 mole of cells would be approximately equivalent to the number of cells found composing every human on earth. (100 trillion cells per person × 7.4 billion people = 7.4×1023 cells)
Practice
Determine
A. the number of C atoms in 12.00 moles of carbon
B. the number of moles of sodium in a sample containing 3.23×1010 Na atoms
Solution
A
\[\begin{align*} \left ( \dfrac{12~\mathrm{mol~C}}{} \right ) \left ( \dfrac{6.022\times 10^{23}~\mathrm{C~atoms}}{1~\mathrm{mol~C}} \right ) = 7.226\times 10^{24}~\mathrm{C~atoms} \end{align*}\]
B
\[\begin{align*} \left ( \dfrac{3.23\times 10^{10}~\mathrm{Na~atoms}}{} \right ) \left ( \dfrac{1~\mathrm{mol~Na}}{6.022\times 10^{23}~\mathrm{Na~atoms}} \right ) = 5.36\times 10^{-14}~\mathrm{mol~Na} \end{align*}\]
The molar mass of a substance is the mass in grams of one mole of the substance. The mass of 1 mole of carbon–12 is exactly 12 g. The mass of 1 carbon–12 atom is exactly 12 amu.
We usually express molar masses in units of grams per mole (g mol–1) to facilitate cancellation of units in calculations. Molar masses can be found on the periodic table. For example, in1 mole of carbon–12, we have:
\[\dfrac{\mathrm{12~g~C}}{\mathrm{1~mol~C}} ~~~~\mathrm{or}~~~~ \dfrac{\mathrm{1~mol~C}}{\mathrm{12~g~C}}\]
Example
How many moles are in 62.8 g of Fe?
\[\left ( \dfrac{62.8~\mathrm{g~Fe}}{} \right ) \left ( \dfrac{1~\mathrm{mol~Fe}}{55.85~\mathrm{g~Fe}} \right ) = 1.12~\mathrm{mol~Fe}\]
Molecular mass (or molecular weight) is the sum of the atomic masses (in amu) in a molecule. For any molecule, molecular mass (amu) = molar mass (grams)
SO2 has a molecular mass of 64.07 amu (this is per molecule of SO2). SO2 has a molar mass of 64.07 g mol–1 (this is per mole of SO2).
Example
How many moles of Ca3(PO4)2 are in 10.0 g of the compound?
\[\left [ (3) \left ( \dfrac{40.08~\mathrm{g~Ca}}{\mathrm{mol~Ca}} \right )\right ] + \left [ (2) \left ( \dfrac{30.97~\mathrm{g~P}}{\mathrm{mol~P}} \right )\right ] + \left [ (8) \left ( \dfrac{16.00~\mathrm{g~O}}{\mathrm{mol~O}} \right )\right ] = 310.18~\mathrm{g~mol^{-1}}\]
\[\left ( \dfrac{10.0~\mathrm{g~Ca_3(PO_4)_2}}{} \right )\left ( \dfrac{1~\mathrm{mol~Ca_3(PO_4)_2}}{310.2~\mathrm{g~Ca_3(PO_4)_2}} \right ) = 0.0322~\mathrm{mol~Ca_3(PO_4)_2}\]
2.6.1 Conversions
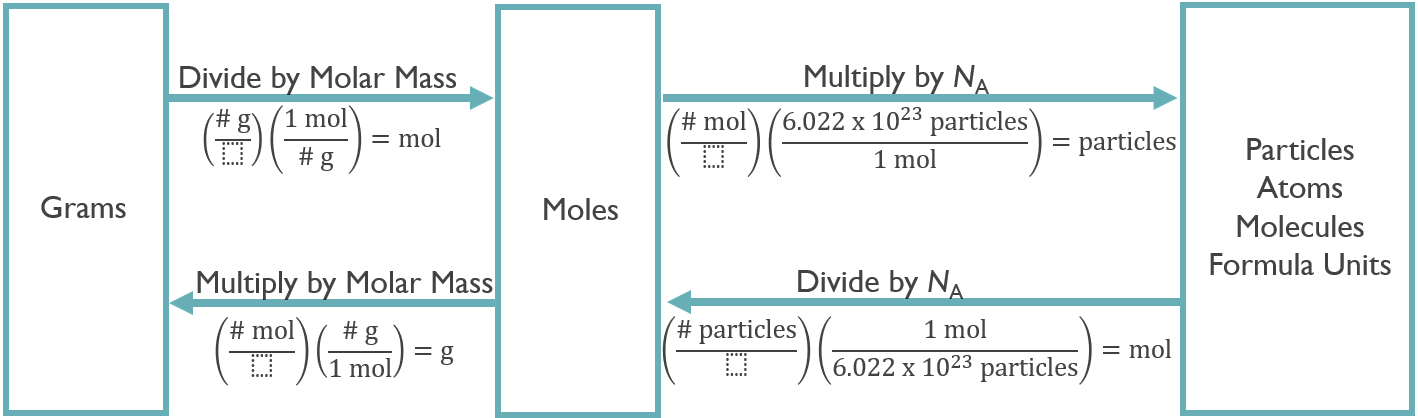
Molar mass is the conversion factor from mass to moles, and vice versa.
Avogadro’s constant converts from moles to atoms.
Practice
Determine
A. the number of Ca atoms in 0.515 g of Ca
B. the mass of H that contains 6.89×1018 H atoms
Solution
A
\[\begin{align*} \left ( \dfrac{0.515~\mathrm{g~Ca}}{} \right ) \left ( \dfrac{1~\mathrm{mol~Ca}}{40.0801~\mathrm{g~Ca}} \right ) \left ( \dfrac{6.022\times 10^{23}~\mathrm{Ca~atoms}}{\mathrm{1~mol~Ca}} \right ) = 7.74\times 10^{21}~\mathrm{Ca~atoms} \end{align*}\]
B
\[\begin{align*} \left ( \dfrac{6.89\times 10^{18}~\mathrm{H~atoms}}{} \right ) \left ( \dfrac{1~\mathrm{mol~H}}{6.022\times 10^{23}~\mathrm{H~atoms}} \right ) \left ( \dfrac{1.008~\mathrm{g~H}}{1~\mathrm{mol~H}} \right ) = 1.15\times 10^{-5}~\mathrm{g~H} \end{align*}\]
Practice
Determine
A. the number of water molecules and the numbers of H and O atoms in 3.26 g of water
B. the mass of 7.92×1019 carbon dioxide molecules
Solution
A
\[\begin{align*} \left ( \dfrac{3.26~\mathrm{g~H_2O}}{} \right ) \left ( \dfrac{1~\mathrm{mol~H_2O}}{18.02~\mathrm{g~H_2O}} \right ) \left ( \dfrac{6.022\times 10^{23}~\mathrm{H_2O~molecules}}{\mathrm{1~mol~H_2O}} \right ) = 1.09\times 10^{23}~\mathrm{H_2O~molecules} \end{align*}\]
Using the molecular formula, we can determine the number of H and O atoms in 3.26 g of H2O as follows:
\[\begin{align*} \left ( \dfrac{1.09\times 10^{23}~\mathrm{H_2O~molecules}}{} \right ) \left ( \dfrac{2~\mathrm{H~atoms}}{1~\mathrm{H_2O~molecule}} \right ) &= 2.18\times 10^{23}~\mathrm{H~atoms}\\[2ex] \left ( \dfrac{1.09\times 10^{23}~\mathrm{H_2O~molecules}}{} \right ) \left ( \dfrac{1~\mathrm{O~atom}}{1~\mathrm{H_2O~molecule}} \right ) &= 1.09\times 10^{23}~\mathrm{O~atoms} \end{align*}\]
B
\[\begin{align*} \left ( \dfrac{7.92\times 10^{19}~\mathrm{CO_2~molecules}}{} \right ) \left ( \dfrac{1~\mathrm{mol~CO_2}}{6.022\times 10^{23}~\mathrm{CO_2~molecules}} \right ) \left ( \dfrac{44.01~\mathrm{g~CO_2}}{1~\mathrm{mol~CO_2}} \right ) = 5.79\times 10^{-3}~\mathrm{g~CO_2} \end{align*}\]