3.2 Electromagnetic radiation
Visible light is only a small component of the continuum of radiant energy known as the electromagnetic spectrum.
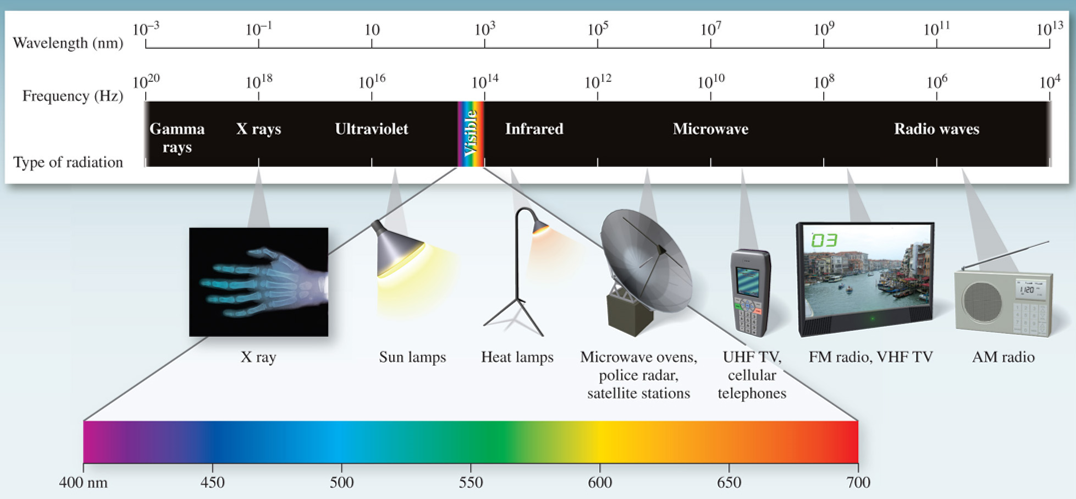
3.2.1 Wave
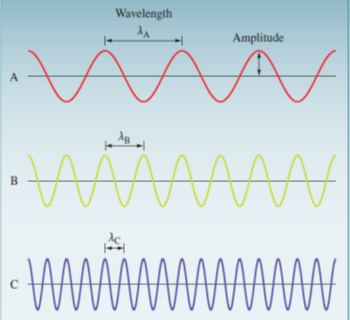
All forms of electromagnetic radiation travel in waves. Waves are characterized by:
- Wavelength (λ) – the distance between identical points on successive waves
- Frequency (ν) – the number of waves that pass through a point in 1 second.
- Amplitude – the vertical distance from the midline of a wave to the top of the peak or the bottom of the trough.
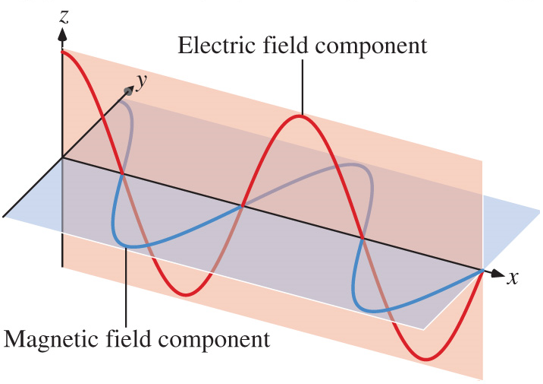
An electromagnetic wave has both an electric field component and a magnetic component.
The electric and magnetic components have the same frequency and wavelength.
A famous experiment known as the Double-slit experiment illustrates the wavelike nature of light. When light passes through two closely spaced slits, an interference pattern is produced. Constructive interference is a result of adding waves that are in phase. Destructive interference is a result of adding waves that are out of phase.

The speed of light (c) through a vacuum is a constant: c = 2.998×108 m s–1. Speed of light, frequency and wavelength are related:
\[c = \lambda\nu\]
where λ is length and ν is reciprocal time (s–1). In SI units, these combined units gives m s–1. Note that s–1 is commonly referred to as the hertz, Hz (i.e. s–1 ≡ Hz).
Practice
What is the frequency (in Hz) of radiation with a wavelength of 280 nm? What is the wavelength (in nm) of light with a frequency of 5.65×1014 Hz?
Solution
Part 1
Convert the wavelength of light from nm to m in order to use the speed of light (in m s–1). Find the frequency.
\[\begin{align*} c &= \lambda\nu \rightarrow \\[2ex] \nu &= \dfrac{c}{\lambda} \\[2ex] &= \dfrac{2.998\times 10^{8}~\mathrm{m~s^{-1}}}{\left ( \dfrac{280~\mathrm{nm}}{} \right ) \left ( \dfrac{1\times 10^{-9}~\mathrm{m}}{\mathrm{nm}} \right )} \\[2ex] &= 1.07\times 10^{15}~\mathrm{s^{-1}} \end{align*}\]
Part 2
Find the wavelength (in nm) for the given frequency of light.
\[\begin{align*} c &= \lambda\nu \rightarrow \\[2ex] \lambda &= \dfrac{c}{\nu} \\[2ex] &= \dfrac{2.998\times 10^{8}~\mathrm{m~s^{-1}}}{5.65\times 10^{14}~\mathrm{s^{-1}}} \left ( \dfrac{1\times 10^{9}~\mathrm{nm}}{\mathrm{m}} \right ) \\[2ex] &= 531~\mathrm{nm} \end{align*}\]
Practice
What is the frequency (in Hz) for 500. nm light?
Solution
\[\begin{align*} c &= \lambda\nu \rightarrow \\[2ex] \nu &= \dfrac{c}{\lambda} \\[2ex] &= \dfrac{2.998\times 10^{8}~\mathrm{m~s^{-1}}}{\left ( \dfrac{500~\mathrm{nm}}{} \right ) \left ( \dfrac{1\times 10^{-9}~\mathrm{m}}{\mathrm{nm}} \right )} \\[2ex] &= 6.02\times 10^{14}~\mathrm{s^{-1}} \\[2ex] &= 6.02\times 10^{14}~\mathrm{Hz} \end{align*}\]
Practice
Assume a microwave oven operates at a frequency of 1.80×1011 s–1.
What is the wavelength (in nm)?
Solution
\[\begin{align*} c &= \lambda\nu \rightarrow \\[2ex] \lambda &= \dfrac{c}{\nu} \\[2ex] &= \dfrac{2.998\times 10^{8}~\mathrm{m~s^{-1}}}{1.80\times 10^{11}~\mathrm{s^{-1}}} \left ( \dfrac{1\times 10^{9}~\mathrm{nm}}{\mathrm{m}} \right ) \\[2ex] &= 1.67\times 10^{-3}~\mathrm{nm} \end{align*}\]
3.2.2 Quantum Theory
Early attempts by nineteenth-century physicists to figure out the structure of the atom met with only limited success. They were using the laws of classical physics. These laws describe the behavior of macroscopic objects.
Over time, the realization and acceptance was the behavior of subatomic particles is NOT governed by the same physical laws as larger objects. This became known as Quantum Mechanics.
When a solid is heated, it emits electromagnetic radiation, known as blackbody radiation, over a wide range of wavelengths. The amount of energy given off at a certain temperature depends on the wavelength. Classical physics assumed that radiant energy was continuous; that is, could be emitted or absorbed in any amount. Max Planck suggested that radiant energy is only emitted or absorbed in discrete quantities, like small packages or bundles. A quantum of energy is the smallest quantity of energy that can be emitted (or absorbed).
3.2.3 Energy and Light
The energy of a single quantum of energy is
\[E = h\nu\]
where Planck’s constant, h, is equal to 6.626×10–34 J·s. The idea that energy is quantized rather than continuous is like walking up a staircase or playing the piano. You cannot step or play anywhere (continuous), you can only step on a stair or play on a key (quantized).
Einstein proposed that the beam of light is really a stream of particles. These “particles” of light are now called photons.
Energy is related to the frequency of light (ν) given as
\[E = h\nu\]
as well as the wavelength (λ) of light given as
\[E = \dfrac{hc}{\lambda}\]
Practice
Calculate the energy (in joules) of
A. a photon with a wavelength of 501 nm
B. a photon with a wavelength of 50.1 nm
Solution
A
\[\begin{align*} E &= \dfrac{hc}{\lambda} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {\left ( \dfrac{501~\mathrm{nm}}{} \right ) \left ( \dfrac{\mathrm{m}}{1\times 10^{9}~\mathrm{nm}} \right )} \\[2ex] &= 3.97\times 10^{-19}~\mathrm{J} \end{align*}\]
B
\[\begin{align*} E &= \dfrac{hc}{\lambda} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {\left ( \dfrac{50.1~\mathrm{nm}}{} \right ) \left ( \dfrac{\mathrm{m}}{1\times 10^{9}~\mathrm{nm}} \right )} \\[2ex] &= 3.97\times 10^{-18}~\mathrm{J} \end{align*}\]
Practice
What is the energy of a photon at 379. nm?
Solution
\[\begin{align*} E &= \dfrac{hc}{\lambda} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {\left ( \dfrac{397~\mathrm{nm}}{} \right ) \left ( \dfrac{\mathrm{m}}{1\times 10^{9}~\mathrm{nm}} \right )} \\[2ex] &= 5.24\times 10^{-19}~\mathrm{J} \end{align*}\]
Practice
What is the energy (in J) of a photon with a frequency of 4.86×1011 s–1?
Solution
\[\begin{align*} E &= h\nu \\[2ex] &= (6.63\times 10^{-34}~\mathrm{J~s})(4.86\times 10^{11}~\mathrm{s^{-1}}) \\[2ex] &= 3.22\times 10^{-22}~\mathrm{J} \end{align*}\]
Practice
What is the frequency (in Hz) of light having an energy of 1.93×10–17 J?
Solution
\[\begin{align*} E &= h\nu \rightarrow \\[2ex] \nu &= \dfrac{E}{h} \\[2ex] &= \dfrac{1.93\times 10^{-17}~\mathrm{J}}{6.63\times 10^{-34}~\mathrm{J~s}} \\[2ex] &= 2.91\times 10^{16}~\mathrm{Hz} \end{align*}\]
Practice
The nitrogen laser emits light at 337.1 nm. What is the energy (in J) of this light?
Solution
\[\begin{align*} E &= \dfrac{hc}{\lambda} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {\left ( \dfrac{337.1~\mathrm{nm}}{} \right ) \left ( \dfrac{\mathrm{m}}{1\times 10^{9}~\mathrm{nm}} \right )} \\[2ex] &= 5.90\times 10^{-9}~\mathrm{J} \end{align*}\]