3.3 Atomic Line Spectra
The emission spectrum of a substance can be seen by energizing a sample of material with some form of energy. The “red hot” or “white hot” glow of an iron bar removed from a fire is the visible portion of its emission spectrum. The emission spectrum of both sunlight and a heated solid are continuous; all wavelengths of visible light are present. Line spectra are the emission of light only at specific wavelengths. Every element has its own unique emission spectrum.
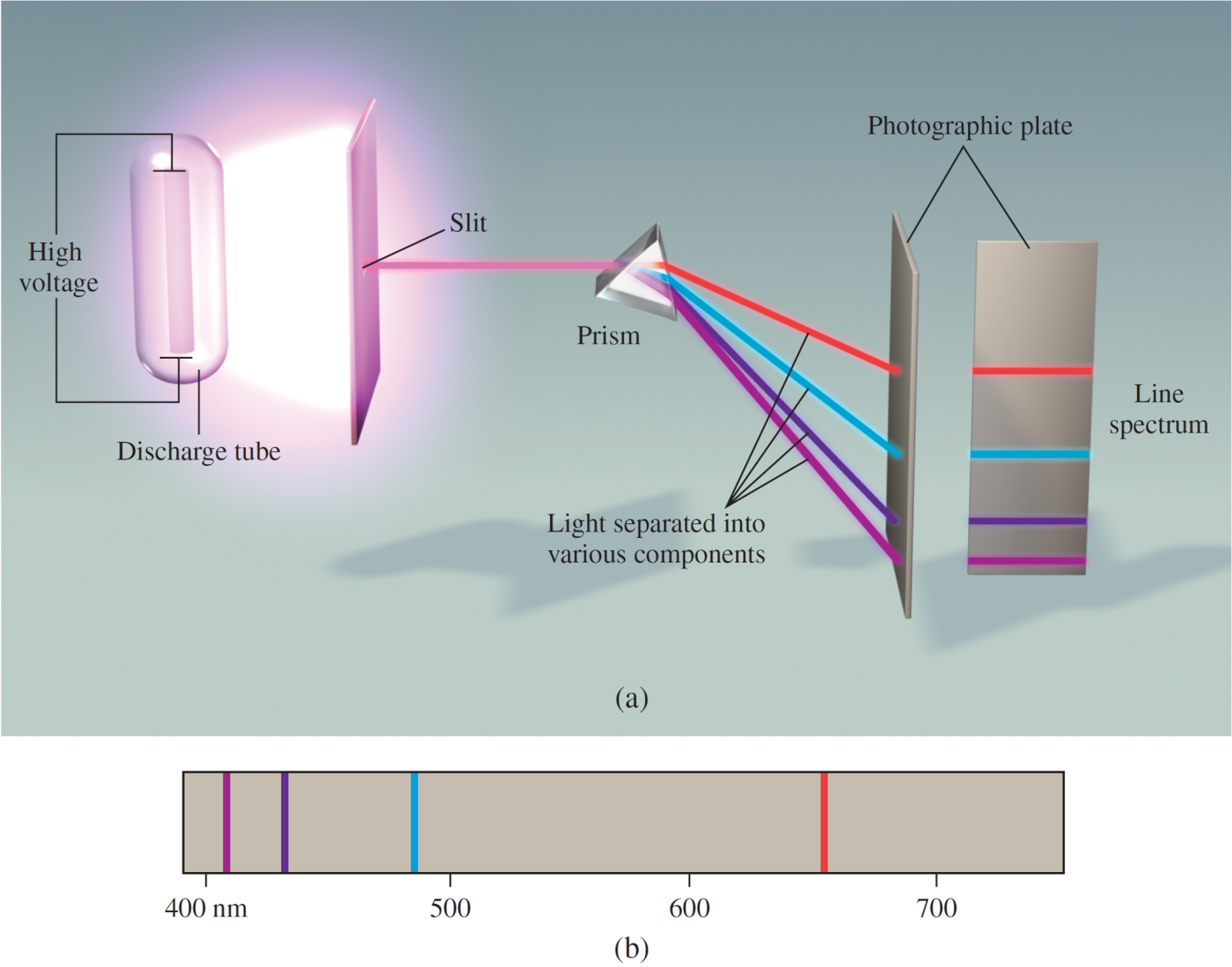
Figure 3.1: Line spectra of hydrogen.
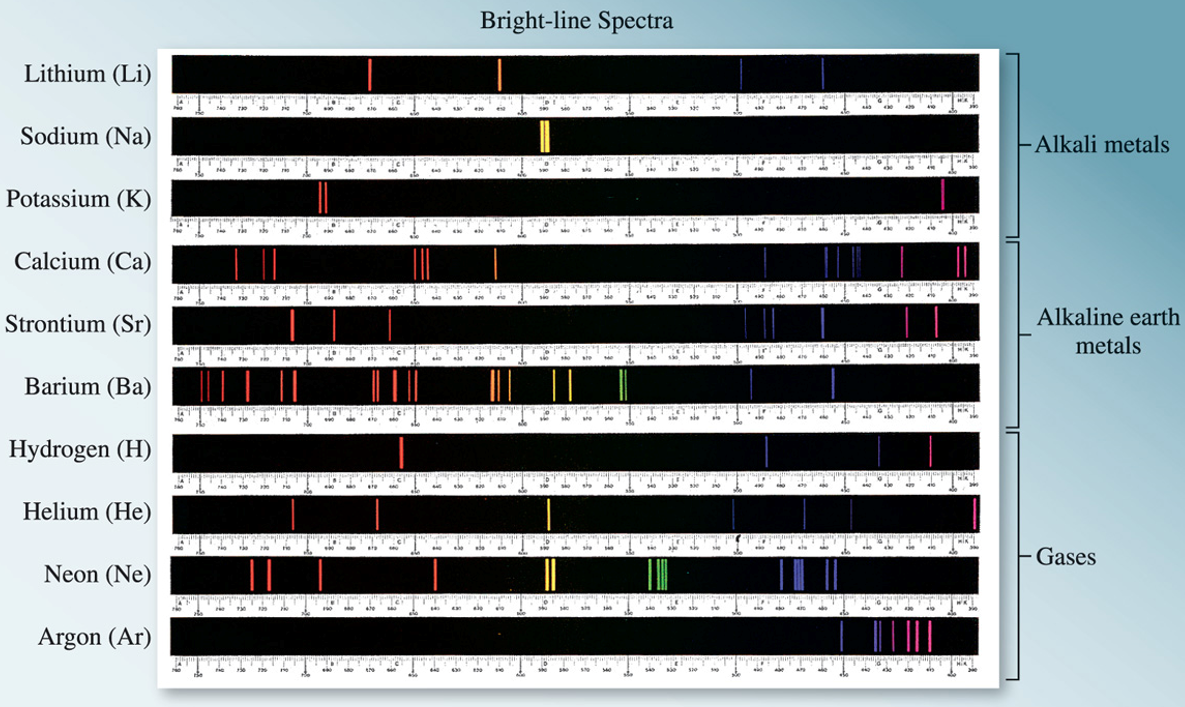
Figure 3.2: Line spectra for various elements.
3.3.1 Rydberg equation
The Rydberg equation can be used to calculate the wavelengths of the four visible lines in the emission spectrum of hydrogen
\[\dfrac{1}{\lambda} = R_{\infty} \left ( \dfrac{1}{n_1^2} - \dfrac{1}{n_2^2} \right )\]
where R∞ is the Rydberg constant (R∞ = 1.09737317×107 m–1), λ is the wavelength of the observed line in the hydrogen emission spectrum, n1 and n2 are positive integers (where n2 > n1).
The associated energy change (ΔE) with respect to the observed wavelength can be expressed as
\[\Delta E = -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right ) \]
where ni is the initial state and nf is the final state. If the energy change is negative, the final state has lower energy than the initial state (energy was lost/emitted; relaxation). If the energy change is positive, the the final state has higher energy than the initial state (energy was absorbed; excitation).
Bohr’s theory explains the line spectrum of the hydrogen atom. Radiant energy absorbed by the atom causes the electron to move from the ground state (n = 1) to an excited state (n > 1). Conversely, radiant energy is emitted when the electron moves from a higher–energy state to a lower–energy excited state or the ground state.
The quantized movement of the electron from one energy state to another is analogous to a ball moving and down steps.
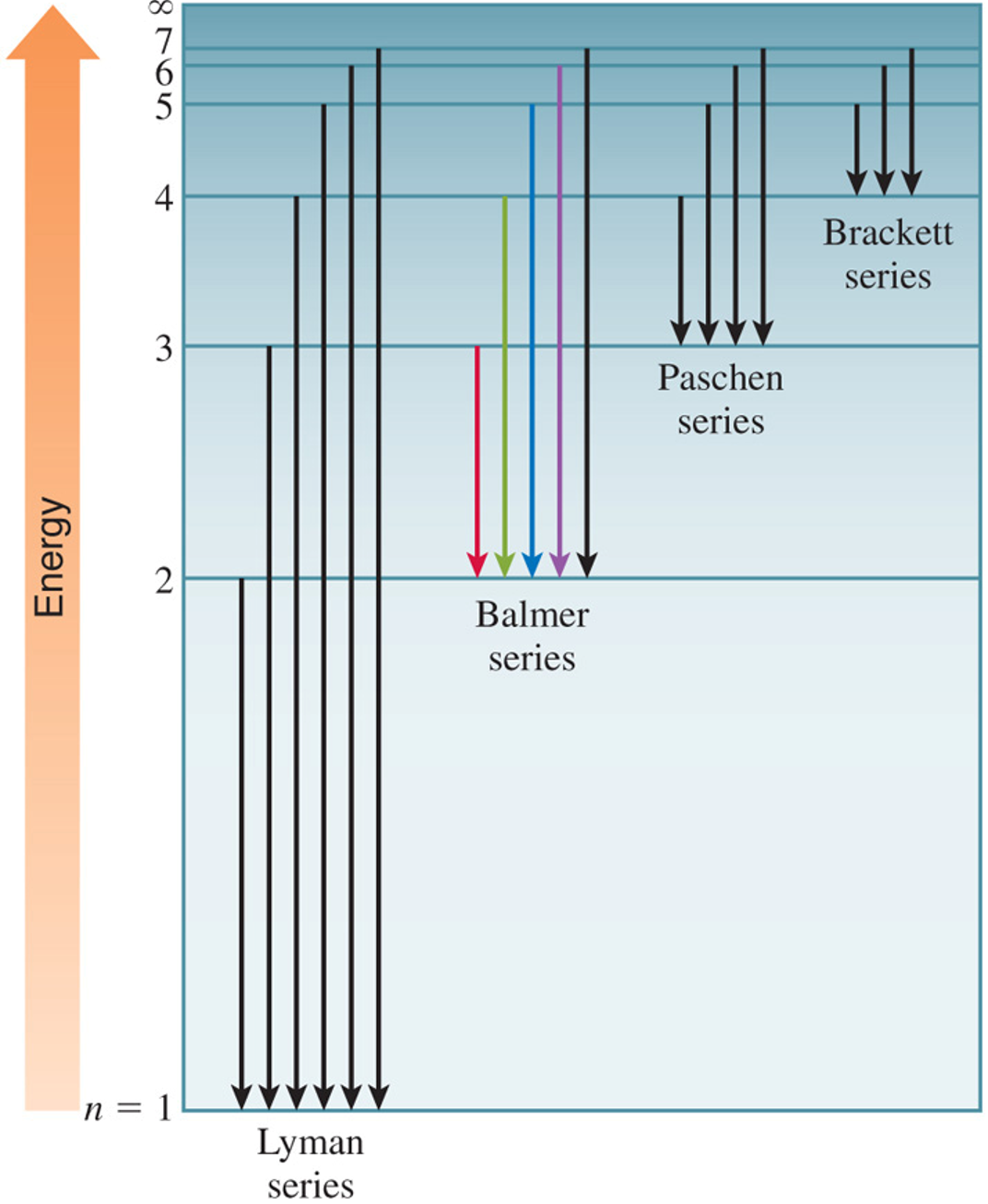
Neils Bohr attributed the emission of radiation by an energized hydrogen atom to the electron dropping from a higher–energy orbit to a lower one. As the electron dropped, it gave up a quantum of energy in the form of light. Bohr showed that the energies of the electron in a hydrogen atom are given by the equation:
\[E_{\mathrm{n}} = -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{n^2} \right )\]
where n is a positive integer. As an electron gets closer to the nucleus, n decreases. En becomes larger in absolute value (more negative) as n gets smaller. En is most negative when n = 1 (called the ground state, the lowest energy state of the atom). The stability of the electron decreases as n increases. Each energy state in which n > 1 is called an excited state.
| Series | nf | ni | Spectrum Region |
|---|---|---|---|
Lyman |
1 |
2,3,4… |
ultraviolet (UV) |
Balmer |
2 |
3,4,5… |
visible and UV |
Paschen |
3 |
4,5,6… |
infrared |
Brackett |
4 |
5,6,7… |
infrared |
Practice
Calculate the wavelength (in nm) of the photon emitted when an electron transitions from the n = 4 state to the n = 3 state in a hydrogen atom.
Solution
Find the energy lost due to the relaxation transition.
\[\begin{align*} \Delta E &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right ) \\[2ex] &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{3^2} - \dfrac{1}{4^2} \right ) \\[2ex] &= -1.060\times 10^{-19}~\mathrm{J} \end{align*}\]
The transition emitted E = 1.060×10–19 J of energy. Convert this to wavelength (in m).
\[\begin{align*} E &= \dfrac{hc}{\lambda} \rightarrow \\[2ex] \lambda &= \dfrac{hc}{E} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {1.060\times 10^{-19}~\mathrm{J}} \\[2ex] &= 1.88\times 10^{-6}~\mathrm{m} \end{align*}\]
Convert the wavelength to nm.
\[\begin{align*} \left ( \dfrac{1.88\times 10^{-6}~\mathrm{m}}{} \right ) \left ( \dfrac{1~\mathrm{nm}}{1.0\times 10^{-9}~\mathrm{m}} \right ) = 1880~\mathrm{nm} \end{align*}\]
Practice
Calculate the ΔE and wavelength (in nm) for an H–atom undergoing an n = 4 to n = 2 transition.
Solution
Find the energy lost due to the relaxation transition.
\[\begin{align*} \Delta E &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right ) \\[2ex] &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{2^2} - \dfrac{1}{4^2} \right ) \\[2ex] &= -4.086\times 10^{-19}~\mathrm{J} \end{align*}\]
The transition emitted E = 4.086×10–19 J of energy. Convert this to wavelength (in m).
\[\begin{align*} E &= \dfrac{hc}{\lambda} \rightarrow \\[2ex] \lambda &= \dfrac{hc}{E} \\[2ex] &= \dfrac{(6.63\times 10^{-34}~\mathrm{J~s})(2.998\times 10^{8}~\mathrm{m~s^{-1}})} {4.086\times 10^{-19}~\mathrm{J}} \\[2ex] &= 4.862\times 10^{-7}~\mathrm{m} \end{align*}\]
Convert the wavelength to nm.
\[\begin{align*} \left ( \dfrac{4.862\times 10^{-7}~\mathrm{m}}{} \right ) \left ( \dfrac{1~\mathrm{nm}}{1.0\times 10^{-9}~\mathrm{m}} \right ) = 486.2~\mathrm{nm} \end{align*}\]
Practice
Calculate the wavelength emitted with an electron changes from n = 6 to n = 2 in the H atom. What is the energy (in J) for that photon? What is the energy for 1 mol of these photons?
Solution
Find the energy lost due to the relaxation transition.
\[\begin{align*} \Delta E &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right ) \\[2ex] &= -2.18\times 10^{-18}~\mathrm{J} \left ( \dfrac{1}{2^2} - \dfrac{1}{6^2} \right ) \\[2ex] &= -4.84\times 10^{-19}~\mathrm{J} \end{align*}\]
The transition emitted E = 4.84×10–19 J of energy.
For one mole of photons, use Avogadro’s number to scale up the energy.
\[\left ( \dfrac{4.84\times 10^{-19}~\mathrm{J}}{\mathrm{photon}}\right ) \left ( \dfrac{6.022\times 10^{23}~\mathrm{photons}}{1~\mathrm{mol}} \right ) \left ( \dfrac{\mathrm{kJ}}{10^3~\mathrm{J}} \right ) = 291.5~\mathrm{kJ~mol^{-1}}\]
3.3.2 Wave properites of matter
Louis de Broglie reasoned that if light can behave like a stream of particles (photons), then electrons could exhibit wavelike properties. According to de Broglie, electrons behave like standing waves. Only certain wavelengths are allowed. At a node, the amplitude of the wave is zero.
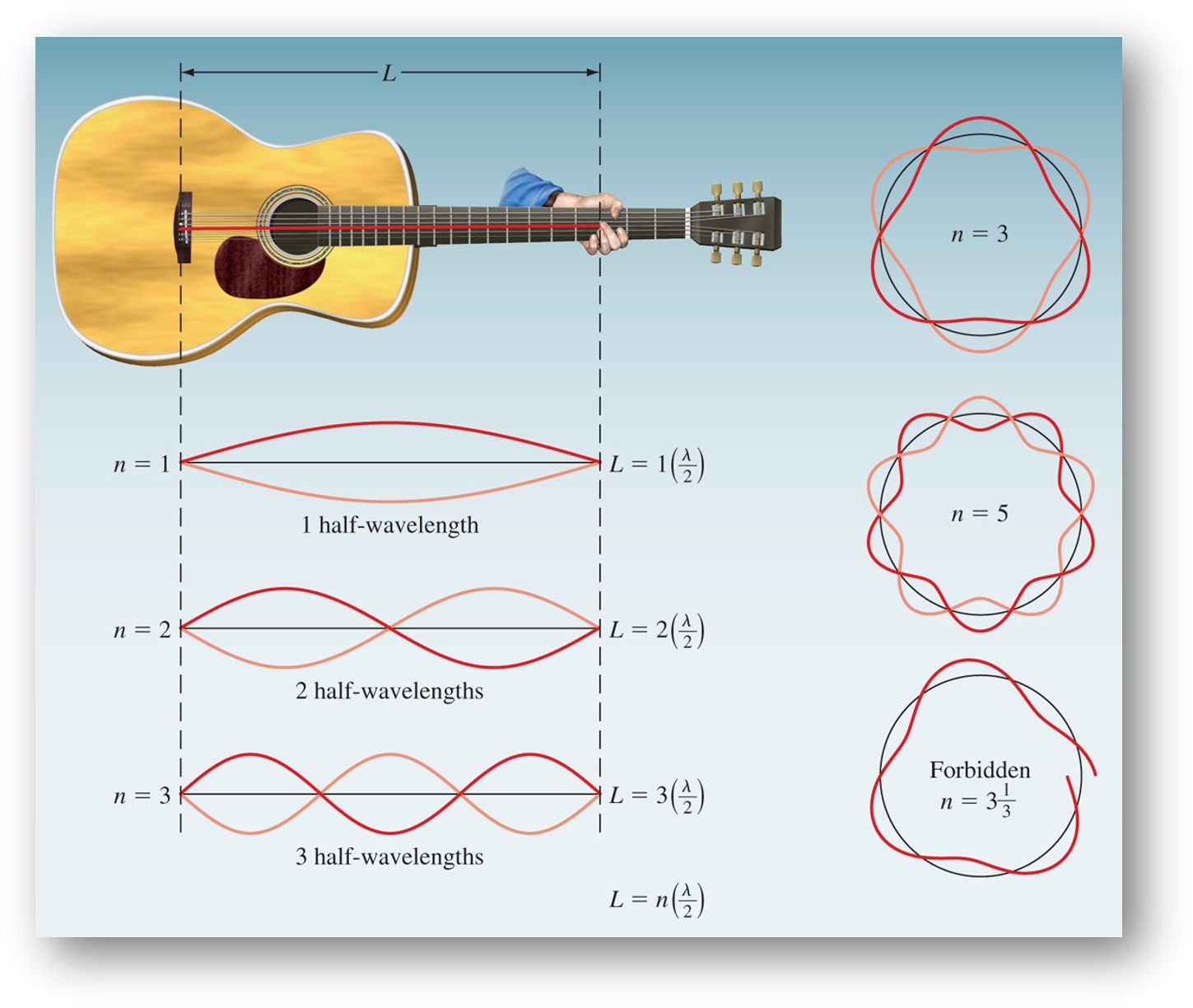
De Broglie deduced that the particle and wave properties are related by the following expression:
\[\lambda = \dfrac{h}{mv}\]
where λ is the de Broglie wavelength of the particle, m is mass, and v is velocity. In SI units, λ is in m, m is in kg, and v is in m s–1.
Practice
Calculate the de Broglie wavelength of the “particle”, when considering a 10.0 g bullet traveling at 762 m s–1.
Solution
The mass (in kg) of a 10.0 g object is 0.0100 kg.
\[\begin{align*} \lambda &= \dfrac{h}{mv} \\[2ex] &= \dfrac{6.63\times 10^{-34}~\mathrm{kg~m^2~s^{-1}}}{(0.0100~\mathrm{kg})(762~\mathrm{m~s^{-1}})} \\[2ex] &= 8.70\times 10^{-35}~\mathrm{m} \end{align*}\]