1.3 Measurements
In America, the English system is used, measurements which include feet, pounds, ounces, etc. These are not universal. In science it is important to have consistency in measurement for easier communication between scientists around the world. To create consistency in measurement, we have a standardized unit of measurement, this standard is known as the international system of units, SI Units.
| SI Base Units | ||
These SI base units, which you must familiarize yourself with, are given in the table above. Because these units are so prevalent to understand the mathematical application of concepts, you must memorize these units and their associated symbols.
As indicated in the chart above, the standard unit of length is the meter. The meter is defined as the distance light in a vacuum travel in 1/299,792,458 of a second. This is about 3 inches longer than a yard, 39.37 inches, or 1.094 yard. Mass is the measure in the amount of matter in an object or sample, and the SI unit for mass is kilogram (kg). One kilogram is defined as the precisely measured values of several fundamental physical constants. An atomic mass unit, amu, is what is used to express the mass of atoms and other very small objects, it is defined as one atomic mass unit is equal to one point six times ten to the negative twenty-four grams:
\[1~\mathrm{amu} = 1.6605378\times 10^{-24}~\mathrm{g}\] The SI base unit for temperature is the kelvin (K). Often, the degree Celsius (°C) is seen in chemistry. The magnitude of kelvin and Celsius is the same but the two have a different set zero point. The conversion between kelvin, Celsius, and Fahrenheit will be shown later in the chapter. The unit of time that is the SI base unit is the second (s).
The magnitude of these units can be tailored based on the application being used. In industry, they make bulk products and therefore use much larger quantities, so they may use the kilogram, kg, for many of their measurements; alternatively, chemists working in a research lab will likely use much smaller quantities and just use the gram, g. The magnitude can be changed based off a prefix. Say that we have a kilogram of substance and a reaction to conduct. We might need only a portion of that kilogram, and therefore it may be more beneficial to know how many grams are contained in that kilogram. For that relationship, we use is the chart below.
| Metric Prefixes | |||
This chart relates each prefix unit to the base unit. In each spot that you see the word (base unit) this is replaced by an SI unit (listed above). For example: liters, seconds, grams, etc. An easy way to remember the different prefixes of the metric chart is the following pneumonic device: The Great Mighty King Hector Died Unexpectedly Drinking Chocolate Milk Many Nights Past. The first letter of each of the prefixes start with the first letter of each word. The chart gives the correlation between each of the prefixes and the base unit.
Each prefix line gives an equality statement, or two different ways of representing the same value. For example, 60 seconds is equal to 1 minute. Both values represent the same amount of time but through two different units. As an example, for the tera-gram prefix line from the chart, would yield an equality statement of:
\[1~\mathrm{Tg} = 1\times 10^{12}~\mathrm{g}\]
This tells us that 1 tera-gram is equal to 1 times ten to the twelfth power grams. Equality statements can be used to make a conversion factor. A conversion factor is a ratio expressed as a fraction that equals 1. Though the values on either side of equal sign are different, the units make them equal (just like 60 seconds = 1 minute). Taking the ratio of the two numbers from the equality statement, it is the same as saying you are putting a number on top of itself. When you put any number on top of itself (take the ratio between the same number) the ratio will be equal to 1. A conversion factor can have either value as the numerator, looking back at our tera-gram example:
\[\dfrac{1~\mathrm{Tg}}{1\times 10^{12}~\mathrm{g}} ~~~~~\mathrm{or}~~~~~ \dfrac{1\times 10^{12}~\mathrm{g}}{1~\mathrm{Tg}}\] Notice that in either ratio, it is still the equal values on top and bottom of the ratio, meaning the same value of 1 is obtained in either form.
Conversion factors from equality statements will allow us to move from one prefix to another. The example below shows how to move between units using conversion factors:
How many kilograms are in 3.6 grams?
First, the relationship between kilograms and grams must be found. This relationship is identified through the conversion chart above, where the equality statement between kilogram and gram is given.
\[1~\mathrm{kg} = 1\times 10^{3}~\mathrm{g}\] This tells us that there are 1000 grams for every 1 kilogram. This is the equality statement we will use to make the necessary conversion factor. For each equality statement there are two possible conversion factors, where either side can be in the numerator.
\[\dfrac{1\times 10^{3}~\mathrm{g}}{\mathrm{kg}} ~~~~~\mathrm{or}~~~~~ \dfrac{1~\mathrm{kg}}{1\times 10^{3}~\mathrm{g}}\] To identify the correct conversion factor, first write down what is given in the problem. This identifies the starting unit, and the problem will identify the ending unit desired. In this case, the starting unit is the gram, the ending unit will be the kilogram. To end with the kilogram, the gram must be canceled. Units are canceled by placing them in opposite positions, one in the numerator and the other in the denominator. The value that we are starting with is 3.6 grams (which will start in the numerator) and we can investigate which conversion factor will cancel the grams:
\[\begin{align*} \left ( 3.6~\mathrm{g} \right ) \left ( \dfrac{1\times 10^{3}~\mathrm{g}}{\mathrm{kg}} \right ) \\[2ex] ~~~\mathrm{or}~~~ \left ( 3.6~\mathrm{g} \right ) \left ( \dfrac{1~\mathrm{kg}}{1\times 10^{3}~\mathrm{g}} \right ) \end{align*}\]
Notice in the first option, both numbers with the grams unit are in the numerator. In the second option, the first gram unit is in the numerator (our starting unit), and the conversion factor’s grams unit is in the denominator. Since we need the grams to cancel to be left with kilograms, the second option is the one that is set up correctly, giving a value of 0.0036 kg.
\[\left ( 3.6~\mathrm{g} \right ) \left ( \dfrac{1~\mathrm{kg}}{1\times 10^{3}~\mathrm{g}} \right ) = 0.0036~\mathrm{kg}\]
It is also important to note that anytime a conversion between prefixes occurs that passes the base unit, you must stop at the base unit before moving to the next prefix. This will lead to two steps in your conversion, instead of just the one shown above. Be sure to pay special attention to assure the correct units cancel out in a multi-step conversion problem. Below is an example of a two-step conversion.
How many nanograms are in 3.6 teragrams?
To move between teragram, Tg, and nanogram, ng, you must pass by the base unit in the table. This means that the first conversion will be to the base unit, a second conversion will then be required to reach the nanograms. The first step is to identify the equality statements for each conversion from the chart. These equality statements will be identified by noting the path that must be taken to get from Tg to g, the first equality statement, and going from g to ng, the second equality statement.
\[1~\mathrm{Tg} = 1\times 10^{12}~\mathrm{g}~~~~\mathrm{and}~~~~1~\mathrm{ng} = 1\times 10^{-9}~\mathrm{g}\]
Again, solving this problem will require first writing down the starting value from the problem, 3.6 Tg. The equality statement containing the unit that the problem is starting with (Tg) is used to cancel the Tg unit. The equality statement that contains tera-gram is 1 Tg = 1×1012 g. To cancel the Tg, the value containing the Tg unit will be placed in the denominator, since the starting value given in the problem (3.6 Tg) is in the numerator. Having the Tg from the equality statement in the denominator will ensure Tg are canceled.
\[\left ( 3.6~\mathrm{Tg} \right ) \left ( \dfrac{1\times 10^{12}~\mathrm{g}}{1~\mathrm{Tg}} \right )\]
Now that the Tg are canceled, the unit we are left in is grams. The problem asks for nanograms, therefore a conversion from grams to nanograms is required. The equality statement that contains both nanograms and grams (1 ng = 1×10-9 g) will be needed to convert from grams to nanograms. Notice from the first conversion written above, the grams are in the numerator. This tells us that the grams of the equality statement will be written in the denominator, shown below:
\[\left ( 3.6~\mathrm{Tg} \right ) \left ( \dfrac{1\times 10^{12}~\mathrm{g}}{1~\mathrm{Tg}} \right ) \left ( \dfrac{1~\mathrm{ng}}{1\times 10^{-9}~\mathrm{g}} \right ) = 3.6\times 10^{21}~\mathrm{ng}\] Now, both the Tg and g units are canceled, and the only unit left is the ng. Since this is what the problem asked for, the conversion is finished with 3.6×1021 ng as the answer.
Practice
Calculate the number of kg that are found in 1.3 g.
Solution
\[\begin{align*} \left ( \dfrac{1.3~\mathrm{g}}{} \right ) \left ( \dfrac{\mathrm{kg}}{10^3~\mathrm{g}} \right ) = 0.0013~\mathrm{kg} \end{align*}\]
Practice
How many Mg are in 43.7 mg?
Solution
\[\begin{align*} \left ( \dfrac{43.7~\mathrm{mg}}{} \right ) \left ( \dfrac{\mathrm{g}}{10^3~\mathrm{mg}} \right ) \left ( \dfrac{\mathrm{Mg}}{10^6~\mathrm{g}} \right ) = 4.37\times 10^{-8}~\mathrm{Mg} \end{align*}\]
Practice
Convert 12.00 in to cm and m.
Solution
Convert in to cm.
\[\begin{align*} \left ( \dfrac{12.00~\mathrm{in}}{} \right ) \left ( \dfrac{2.54~\mathrm{cm}}{\mathrm{in}} \right ) = 30.48~\mathrm{cm} \end{align*}\]
Convert cm to m.
\[\begin{align*} \left ( \dfrac{30.5~\mathrm{cm}}{} \right ) \left ( \dfrac{\mathrm{m}}{100~\mathrm{cm}} \right ) = 0.3048~\mathrm{m} \end{align*}\]
Practice
Convert 20.0 mg of gold into lb.
Solution
\[\begin{align*} \left ( \dfrac{20.0~\mathrm{mg}}{} \right ) \left ( \dfrac{\mathrm{g}}{1000~\mathrm{mg}} \right ) \left ( \dfrac{\mathrm{lb}}{453.6~\mathrm{g}} \right ) &= 0.0000441~\mathrm{lb} \\ &= 4.41\times 10^{-5}~\mathrm{lb} \end{align*}\]
Practice
An average adult has 5.20 L of blood. What is the volume of blood in pints?
Solution
\[\begin{align*} \left ( \dfrac{5.20~\mathrm{L}}{} \right ) \left ( \dfrac{10^3~\mathrm{mL}}{\mathrm{L}} \right ) \left ( \dfrac{\mathrm{cup}}{236.5882~\mathrm{mL}} \right ) \left ( \dfrac{1\mathrm{pt}}{2~\mathrm{cup}} \right ) = 10.9~\mathrm{pt} \end{align*}\]
1.3.1 Volume and Density
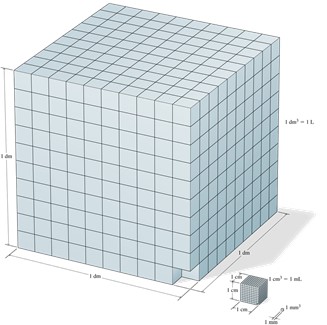
Volume is the measure of the amount of space occupied by an object and the standard volume is a cubic meter (m3), or a cube with edge length of exactly 1 meter. The most used volume is a cubic decimeter (dm3) and it is also known as a liter (L). As a reference for this volume, one liter is equal to about 1.06 quarts. A cubic centimeter (cm3), also known as a milliliter (mL) can also be used to express volume.
Volume and mass are used to determine the density of an object. Density is the ratio of mass to volume, mass divided by volume. The equation for density is below:
\[d = \dfrac{m}{V}\] Here, d represents density, m is mass, and V is volume. To find density, the mass and volume is needed. As mentioned earlier, the derived SI unit for volume is the meter cubed, but the easier unit for us to use is the liter. Knowing the relationship between the dm3 and liter is due to the various object shapes that density will be calculated for. There are two different object shapes to find the volume of, regularly shaped and irregularly shaped.
Finding the volume of a regularly shaped object such as a cube, there is an equation that can be used, alongside measurements, to calculate that volume. If we use an equation for this calculation, we will have some measurement containing the length base unit (such as the dm3). This is done for any regularly shaped object such as a sphere, cylinder, etc. Knowing the relationship between dm3 and liter gives the ability to move from length measurement derivatives to liters.
If the volume of an irregularly shaped object needs to be found a technique called volume displacement is used. This technique uses a known volume of a liquid inside of a container and the irregularly shaped object is added to that liquid inside of the container (ensuring the entire object is submerged into the liquid. The new volume of the liquid is then measured. The difference between the volume after the object is added and before the object is added will give the volume of the object. Using volume displacement, volume is usually given in milliliters or liters.
[TODO: INSERT VOLUEM DISPLACMENT PICTURE]
It is also important to know the different ways that the units can be written out. Below you will see how the units for density can be written as a fraction. These fractions can be written instead as a single line, utilizing a negative exponent to bring them into the numerator. This is how you will likely see the units written for on questions or in exams. Both forms represent the same thing.
\[\begin{align*} &\mathrm{Solids:} &&\dfrac{\mathrm{g}}{\mathrm{cm^3}} &&&\mathrm{or} &&&&\mathrm{g~cm^{-3}}\\[2ex] &\mathrm{Liqiuds:} &&\dfrac{\mathrm{g}}{\mathrm{mL}} &&&\mathrm{or} &&&&\mathrm{g~mL^{-1}}\\[2ex] &\mathrm{Gases:} &&\dfrac{\mathrm{g}}{\mathrm{L}} &&&\mathrm{or} &&&&\mathrm{g~L^{-1}} \end{align*}\]
Practice – Volume
An irregularly shaped sample of aluminum (Al) is put on a balance and found to have a mass of 43.6 grams. The student decides to use the water displacement method to find the volume of the Al sample. The initial volume reading is 25.5 mL, and after the Al sample is added, the water level rose to 41.7 mL. Find the density of the aluminum sample in grams per cubic centimeter.
Solution
This problem is asking for the density of the aluminum sample. Remembering that density is mass over volume, both the mass and volume of the Al sample is needed. The mass is given in the problem, 43.6 grams. To find the volume of the object, volume displacement will be used. The final volume (the volume after Al addition) minus the initial volume of the water (prior to the Al addition). The final volume is 41.7 mL and the initial volume is 25.5 mL, the difference between these is 16.2 mL.
\[\begin{align*} 41.7~\mathrm{mL} - 25.5~\mathrm{mL} = 16.2~\mathrm{mL} \end{align*}\]
Now the volume of the object is known. The last step is to find the density. Substitute in the known mass of 43.6 g and devise that mass by the object’s volume, 16.2 mL.
\[\begin{align*} d &= \dfrac{43.6~\mathrm{g}}{16.2~\mathrm{mL}} \\[2ex] &= \dfrac{2.69~\mathrm{g}}{\mathrm{mL}} \\[2ex] &= \dfrac{2.69~\mathrm{g}}{\mathrm{cm^3}}\\[2ex] &= 2.69~\mathrm{g~cm^{-3}} \end{align*}\]
The density is 2.69 grams per cubic centimeter. Remember that 1 mL = 1 cm3, so a direct substitution is possible to get to the desired final units.
Practice – Volume
A 246.2 g cube of an unknown metal, has an edge measurement of 0.12 m. What is the density (in g mL–1) of this metal?
Solution
Get the volume of the cube.
\[\begin{align*} V &= l \times w \times h \\[2ex] &= (0.12~\mathrm{m})(0.12~\mathrm{m})(0.12~\mathrm{m}) \\[2ex] &= (0.12~\mathrm{m})^3 \\[2ex] &= 0.001728~\mathrm{m^3} \end{align*}\]
Find the density.
\[\begin{align*} d &= \dfrac{m}{V} \\[2ex] &= \dfrac{246.2~\mathrm{g}}{0.001728~\mathrm{m^3}}\\[2ex] &= 1.42\times 10^{5}~\mathrm{g~m^{-3}} \end{align*}\]
Convert the density from g m–3 to g cm–3.
\[\begin{align*} \left ( \dfrac{1.42\times 10^{5}~\mathrm{g}}{\mathrm{m^3}} \right ) \left ( \dfrac{\mathrm{m^3}}{100~\mathrm{cm^3}} \right ) = 0.142~\mathrm{g~cm^{-3}} = 0.142~\mathrm{g~mL^{-1}} \end{align*}\]
Practice
A piece of metal has a mass of 215.8 g. When placed into a measuring cylinder, it displaces 19.1 mL of water. Identify the metal using the densities given below (at 20 °C).
| Substance | d (g mL–1) |
|---|---|
Magnesium |
1.74 |
Aluminum |
2.70 |
Titanium |
4.50 |
Copper |
8.93 |
Lead |
11.34 |
Mercury |
13.55 |
Gold |
19.32 |
Solution
\[\begin{align*} d &= \dfrac{m}{V} \\[2ex] &= \dfrac{215.8~\mathrm{g}}{19.1~\mathrm{mL}} \\[2ex] &= 11.3~\mathrm{g~mL^{-1}} \end{align*}\]
The metal is lead.
Practice
What is the density of CO gas if 0.196 g occupies a volume of 100 mL?
Solution
\[\begin{align*} d &= \dfrac{m}{V} \\[2ex] &= \dfrac{0.196~\mathrm{g}}{100~\mathrm{mL}} \\[2ex] &= 0.00196~\mathrm{g~mL^{-1}} \end{align*}\]
Practice
An irregularly-shaped sample of aluminum (Al) is put on a balance and found to have a mass of 43.6 g. The student decides to use the water-displacement method to find the volume. The initial volume reading is 25.5 mL and, after the Al sample is added, the water level has risen to 41.7 mL. Find the density of the Al sample in g cm–3.
Solution
\[\begin{align*} d &= \dfrac{m}{V} \\[2ex] &= \dfrac{43.6~\mathrm{g}}{(41.7 - 25.5)~\mathrm{mL}} \\[2ex] &= 2.69~\mathrm{g~mL^{-1}} \\[2ex] &= 2.69~\mathrm{g~cm^{–3}} \end{align*}\]
Practice
Gasoline is a non-polar liquid that will float on water. 450 g of gasoline is spilled into a puddle of water. If the density of gasoline is 0.665 g mL–1, what volume of gasoline is spilled?
Solution
\[\begin{align*} d &= \dfrac{m}{V} \longrightarrow \\[2ex] V &= \dfrac{m}{d} \\[2ex] &= \dfrac{450~\mathrm{g}}{0.655~\mathrm{g~mL^{-1}}} \\[2ex] &= 677~\mathrm{g~mL^{-1}} \end{align*}\]
Practice
A cup of gold colored metal beads was measured to have a mass of 425 g. By water displacement, the volume of the beads was calculated to be 48.0 cm3. Given the following densities (in g mL–1), identify the metal.
- dcopper = 8.86
- dbronze = 9.87
- dgold = 19.3
Solution
\[\begin{align*} d &= \dfrac{m}{V}\\[2ex] &= \dfrac{425~\mathrm{g}}{48.0~\mathrm{cm^{3}}} \\[2ex] &= 8.85~\mathrm{g~cm^{-3}} \\ &= 8.85~\mathrm{g~mL^{-1}} \end{align*}\]
The metal is copper.
Practice
Calculate the mass of a liquid with a density of 3.2 g mL–1 and a volume of 25 mL.
Solution
\[\begin{align*} d &= \dfrac{m}{V} \longrightarrow \\[2ex] m &= dV \\ &= \left ( \dfrac{3.2~\mathrm{g}}{\mathrm{mL}} \right ) \left ( 25~\mathrm{mL} \right ) \\ &= 80~\mathrm{g} \end{align*}\]
Practice
Find the volume that 35.2 g of carbon tetrachloride (CCl4) will occupy if it has a density of 1.60 g mL–1.
Solution
\[\begin{align*} d &= \dfrac{m}{V} \longrightarrow \\[2ex] V &= \dfrac{m}{d} \\[2ex] &= \dfrac{35.2~\mathrm{g}}{1.60~\mathrm{g~mL^{-1}}} \\[2ex] &= 22.0~\mathrm{mL} \end{align*}\]
Practice
HCl(g) has a density of 0.00149 g mL–1 under normal conditions. If you have a mass of 7.85 g of HCl, what is the volume (in L and in gal)?
Solution
Determine the volume of HCl (in mL).
\[\begin{align*} d &= \dfrac{m}{V} \longrightarrow \\[2ex] V &= \dfrac{m}{d} \\[2ex] &= \dfrac{7.85~\mathrm{g}}{0.00149~\mathrm{g~mL^{-1}}} \\[2ex] &= 5.27\times 10^{3}~\mathrm{mL} \end{align*}\]
Convert mL to L.
\[\left ( \dfrac{5.27\times 10^{3}~\mathrm{mL}}{} \right ) \left ( \dfrac{\mathrm{L}}{10^{3}~\mathrm{mL}} \right ) = 5.27~\mathrm{L}\]
Convert L to gal.
\[\left ( \dfrac{5.27~\mathrm{L}}{} \right ) \left ( \dfrac{\mathrm{gal}}{3.785412~\mathrm{L}} \right ) = 1.39~\mathrm{gal}\]
Practice – Density
While working in the laboratory, you were measuring some water in a graduated cylinder. The graduated cylinder reading was 25.0 mL. An unknown metal fell into the graduated cylinder. You looked at the object in the graduated cylinder and noticed that the solution was now at 31.25 mL. You had no idea what this metal was, so you took it out of the graduated cylinder and dried it off. You placed it on a balance and found its mass to be 120.625 g. What is the density (in g mL–1) of the unknown metal?
Solution
Determine the water displaced (in mL) by the metal.
\[\begin{align*} V_{\mathrm{displaced}} &= V_{\mathrm{final}} - V_{\mathrm{initial}} \\ &= 31.25~\mathrm{mL} - 25.0~\mathrm{mL} \\ &= 6.25~\mathrm{mL} \end{align*}\]
Determine the density of the metal.
\[\begin{align*} d &= \dfrac{m}{V} \\[2ex] &= \dfrac{120.625~\mathrm{g}}{6.25~\mathrm{mL}} \\[2ex] &= 19.3~\mathrm{g~mL^{-1}} \end{align*}\]